Linear Regression and Further Analysis of Covid-19

by Jolly Nanda | Apr 9, 2020 | Covid

We now notice that the way in which Covid-19 is spreading no longer fits the exponential model – which is great news as that means that we have likely avoided the worst-case scenario. In this article, we will now move forward trying to analyze the most likely scenario using linear regression to predict the spread of Covid-19 at the national and state level. We had published 3 scenarios for each state. We are now tracking at the most likely model which we had already published on our website.

By Ayesha Rajan, Research Analyst for Altheia Predictive Health

Linear and exponential regression are similar but note that while the equation used for exponential regression is y=ab^x, the equation used for linear regression is y=a+bx. Based on our findings in the last article, we will start our linear regression at or near the date at which the total number of cases falls away from the exponential curve.

Data, Analysis and Discussion

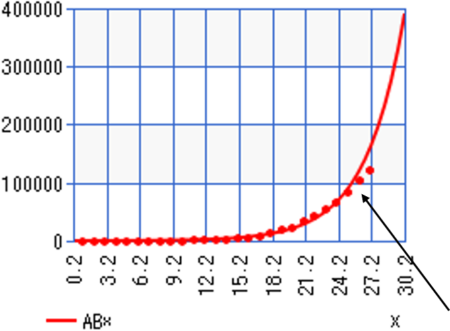
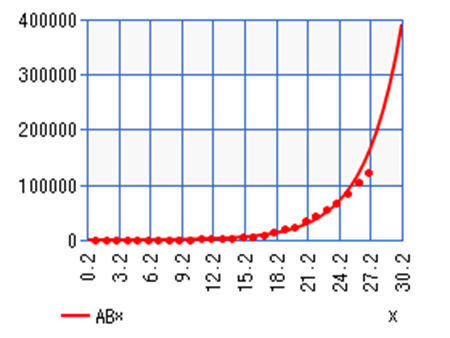
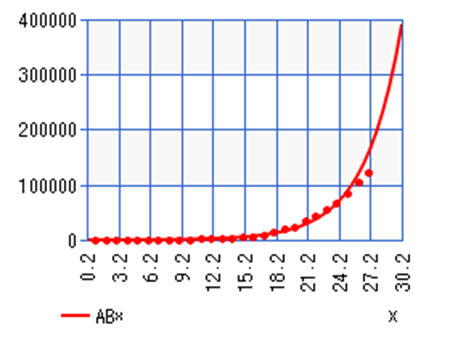
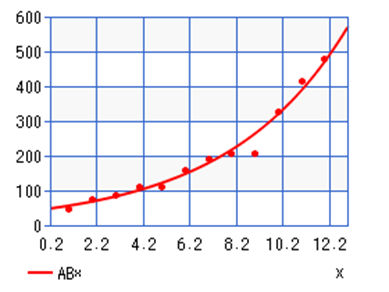
Below is a graph using exponential regression from our last article:

Total Covid-19 Cases in the United States March 4th- 26th  (Exponential Regression)

From this, we can see that the number of cases begins to fall away from the exponential curve around day 25 which was March 26^th, 2020. That is the day we will label as Day 1 in this article. If we started from the same start point (March 2^nd, 2020) as this graph then we would see skewed results that take the initial exponential nature into account; so, here is the new table of data we are working with:

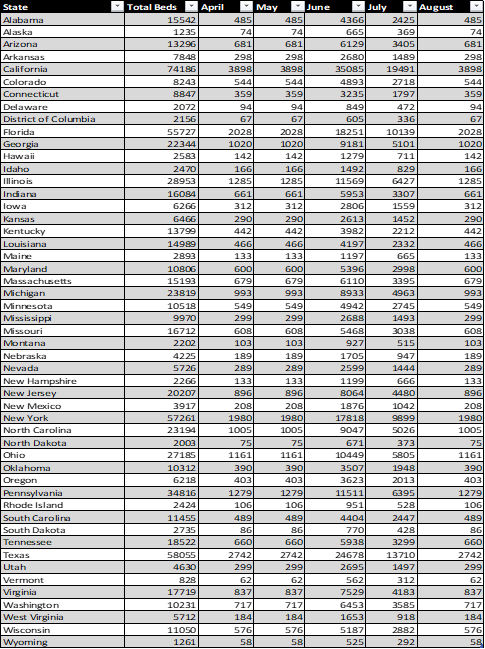
 Total Number of Covid-19 Cases in the United States

Day	Date	Total Number of Cases (y)
1	March 25th, 2020	68,211
2	March 26th, 2020	85,435
3	March 27th, 2020	104,126
4	March 28th, 2020	123, 578
5	March 29th, 2020	143, 491
6	March 30th, 2020	163, 788
7	March 31st, 2020	188, 530
8	April 1st, 2020	215, 003
9	April 2nd, 2020	244, 877
10	April 3rd, 2020	277, 161
11	April 4th, 2020	311, 357
12	April 5th, 2020	336,673
13	April 6th, 2020	367,004
14	April 7th, 2020	400, 335
15	April 8th, 2020	434, 927

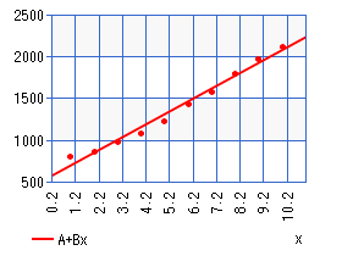
Here is the resulting graph:

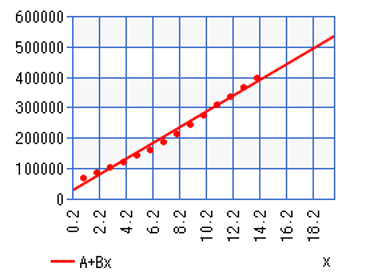From this data, we have that a = 19,255.7429 and b= 26,463.83214. Though it may look like points jump over and under the line a bit, we can see a much tighter fit to the curve and also have a strong correlation coefficient at r = 0.994506795. From this, we can model out the next week as follows:

Day	Date	Predicted Total Cases (y)
17	April 10th, 2020	410,249
18	April 11th, 2020	436,096
19	April 12th, 2020	461,943
20	April 13th, 2020	487,790
21	April 14th, 2020	513,637
22	April 15th, 2020	539,483
23	April 16th, 2020	565,330

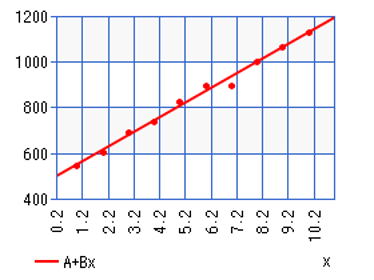
We can see that compared against last week’s prediction and actual case numbers these predictions seem much more realistic. If we analyze at the state level, we can see that some states are still on the initial exponential curve while others have become more linear as well.

In our last article we looked New York, Alabama, Colorado, Missouri, Louisiana and Oregon. Of these states, New York, Louisiana, Colorado and Oregon had a close fit to an exponential curve, though New York seemed to move away from the curve at or around March 24th. The data from Alabama and Missouri did not fit the exponential curve as well as the states mentioned.

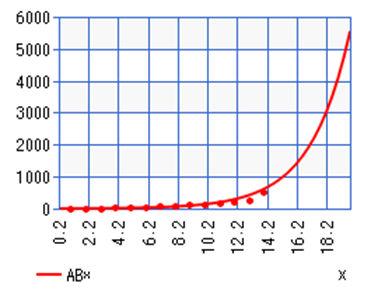
Total Covid-19 Cases in New York March 28th– April 7th For New York’s linear regression equation, we have y=11,980.97143+8,308.503571x.

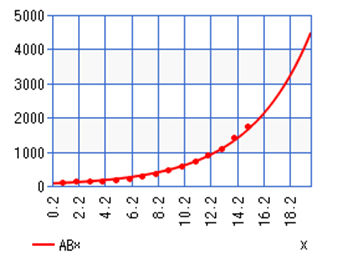
Total Covid-19 Cases in Louisiana March 28th– April 7th For Louisiana’s linear regression equation, we have y=1,239.06667+1,507.987879x.

 

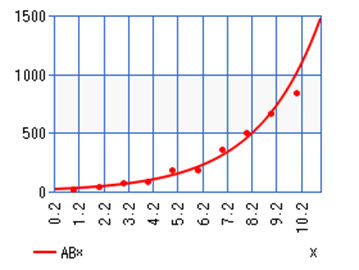
Total Covid-19 Cases in Alabama March 29th– April 7th y=539.66667+153.715515x	Total Covid-19 Cases in Missouri March 29th– April 7th y=606.2+237.8x
Total Covid-19 Cases in Colorado March 29th- April 7th y=487.06667+64.22424242x	Total Covid-19 Cases in Colorado March 29th- April 7th y=1,689.26667+351.2242424x

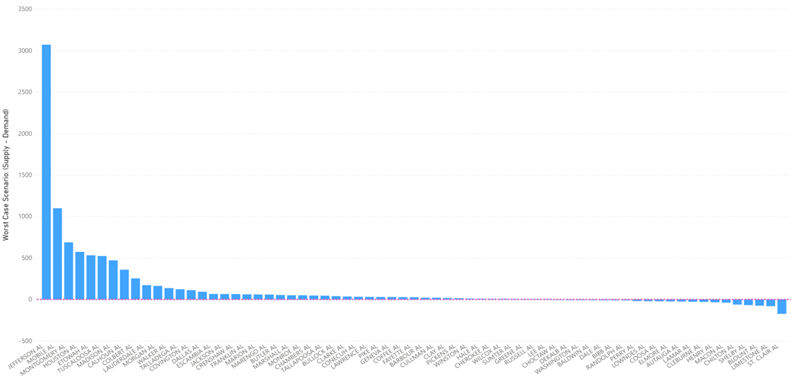
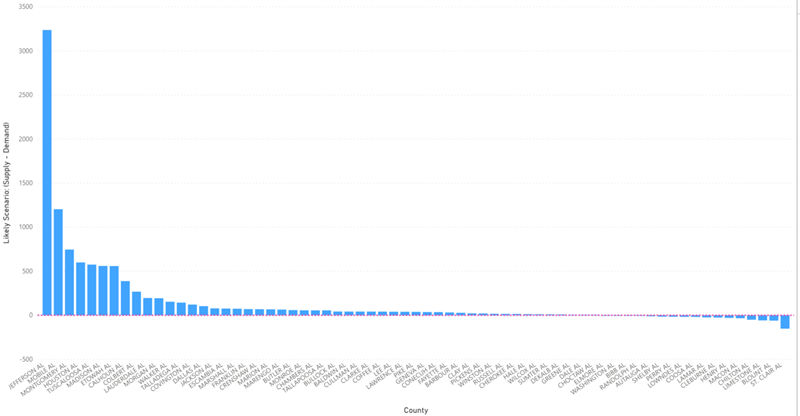
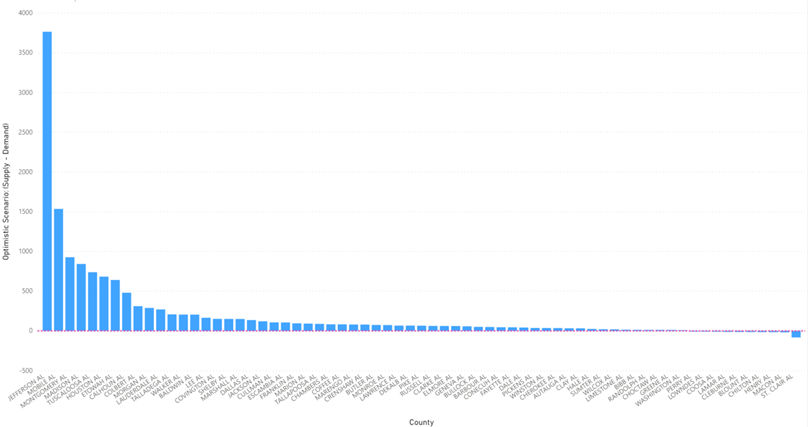
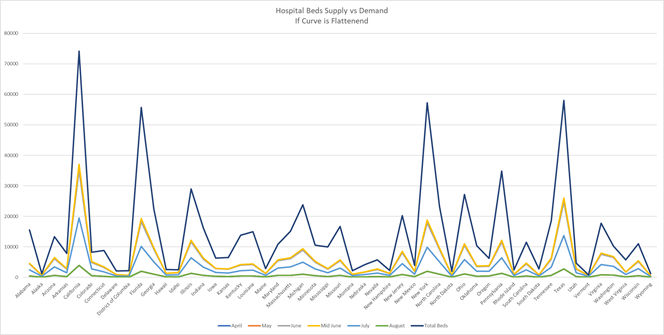
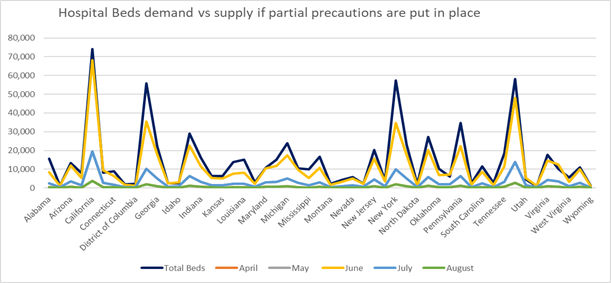
Recall from the last article the Imperial College Study that we used to predict demand for hospital beds. In the study, there were three possible scenarios based on levels of precautions taken: Optimistic Case, Most Likely Case and Worst Case. From the linear regression calculations done here, we can try to see which scenario we are leaning towards given the current situation and data. We will only predict up to June 1^st as, according to the Imperial College Model, that is the latest peak we would see amongst all scenarios.

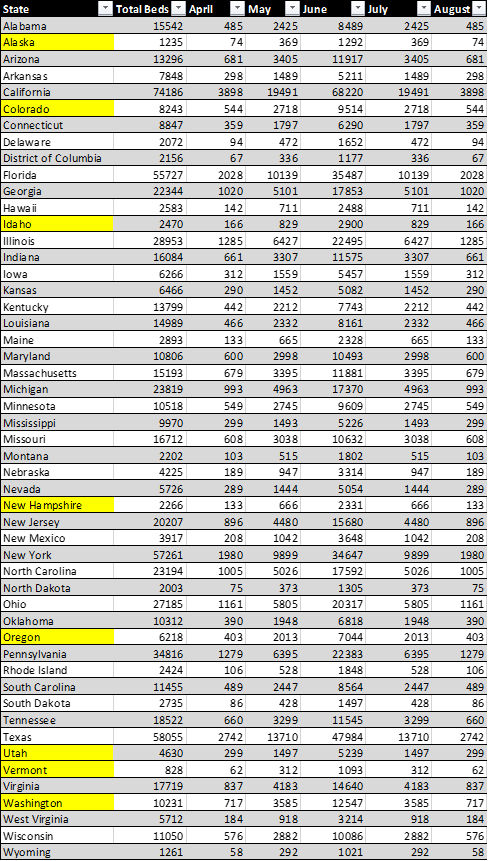
Predicted Total Covid-19 Cases in Six Example States

	May (1st)	Mid – May (15th)	June (1st)
New York	336,012	452,331	593, 576
Louisiana	54,018	75, 130	100,766
Alabama	5, 765	7,918	10,531
Missouri	8,691	12,020	16,063
Oregon	2,670	3,569	4,661
Colorado	13, 630	18, 548	24, 518

From STAT News, 5% of the total cases will need to be hospitalized so we can update the table as follows. Taking that into account, we need to look at the difference in the number of total cases between each month so we can see the number of new cases and then take 5% of that number to get the following table:

Predicted Increase in Demand for Hospital Beds Based on Linear Regression in Six Example States

	April 15th– May 1st	May 1st– 15th	May 15th – June 1st
New York	6,646	5,815	7,062
Louisiana	829	1055	1,281
Alabama	122	107	130
Missouri	190	166	202
Oregon	50	45	55
Colorado	281	245	299

The delta change in demand for hospital beds in New York from May to June in Imperial College’s best case scenario is 15,838. In the worst case scenario it is 32,667. According to our own calculations, it is 19,523. As more data comes in, this could change but as of right now, it seems that we are falling somewhere between Imperial College’s best and most likely scenarios. This holds true for the rest of the states we have looked at as well with some even falling below the best case scenario.

Conclusion
From our own calculations, it seems clear that social distancing and closure precautions are working – the fact that number of cases is falling away from the exponential curve is proof of that. However, despite the fact that the number of cases and demand for hospital beds is optimistic, that does not ensure that certain hospitals will not be overwhelmed. Even in the best case scenario, many hospitals in smaller counties will still fall short of demand for hospital beds.

Citations
Begley, Sharon. “Coronavirus Model Shows Individual Hospitals What to Expect.” STAT, 16 Mar. 2020, www.statnews.com/2020/03/16/coronavirus-model-shows-hospitals-what-to-expect/.

 

Predicting the Effect of Covid-19 on the US Population and Healthcare System

by Jolly Nanda | Mar 30, 2020 | Covid

This article focuses on a simple exponential regression fit to predict the day by day total cases of Covid-19 in the United States, as well as a discussion regarding how this will affect the American population given the worst-case scenario. We have also analyzed the number of hospital beds available at a county level and the capacity to handle these Covid-19 cases. There are a few sample states with county data in this article but we have published all 50 states at our website.

By Ayesha Rajan, Research Analyst for Altheia Predictive Health

Data, Analysis and Discussion

For data collection, I used Worldometer’s “Total Coronavirus Cases in the United States” graph, starting from March 2^nd, to create the following table.

The next step was to simply plug this information into a calculator which then provides two variables, “a” and “b”, such that the function can predict the total number of Covid-19 -19 cases by day. At the time, we have a= 73.5911229 and b= 1.328563895 and as each day goes on, we can add more data and improve accuracy. As such, we could expect the next few days to look something like this:

We could expect to see these numbers, but it is unlikely for reasons we will discuss below. Although it is great information for us to know on the national level, however, it is ultimately too broad to be actionable or even entirely accurate. Analysis at the state and county level can give hospitals a much more accurate idea of spread in each specific area. Exponential regression is very easy to do on a scientific calculator by simply plugging in inputs, x and y, as I did in the table above. There are also several online calculators with the same abilities. At that point, states can better prepare for demand for hospital beds and ventilators.

For example, let us look at New York which has been hit hard by Covid-19. If we set up the table as above for New York, we can see the following:

From this table, we find that in the format, a= 10.08977392 and b= 1.45480788. We can then make the same predictions we did on the national level at the state level. For comparison, let’s look at a different state – Alabama.

For this table, we find that in the format, a= 3.163963707 and b= 1.458356752. Compare these variables, a and b, to that of New York and look at Day 14 in either state – it is instantly clear the importance of making predictions at a more specific regional level.

However, there are flaws to this methodology; take a look at the graphs on the next page. I’ve also included graphs for Colorado, Missouri, Louisiana and Oregon for further comparison.

Looking at these graphs, we begin to see some issues in the use of exponential regression for prediction and the importance of recognizing that is a tool for predicting the worst-case scenario. What we can see here is that the most recent points for the United States and New York are beginning to stray away from the predicted exponential curve – this is a hopeful indication that precautions, such as social distancing and the closing of schools and non-essential businesses, are working and that the curve is flattening. However, if we look at Colorado, Louisiana, and Oregon we can see that there is much better fit to the exponential curve and that, at least for now, these states will likely see more benefit to using exponential regression than states where the curve is beginning to flatten.

With that in mind, it is important to adjust these predictive functions as new data becomes available to keep them as accurate as possible. If this trend seen in the graph of national cases continues, it will become more fitting to move forward with prediction using linear, rather than exponential, regression. It is also important to note that we are not necessarily seeing exponential growth in every area. For example, we can see in the graph for cases in Alabama that the points do not fit the exponential curve as well as the points mapped for national cases or cases in New York. This could mean that we are not yet at the point of exponential growth and will need to add more data each day to see a better fit; or that the spread in Alabama does not have the same rate of spread as in New York due to other factors, such as New York being more densely populated, having more visitors, etc.

The reason we used exponential regression for this article is because of the documented exponential nature of infection in Italy and China. While this method of prediction can work in the short term and help us allocate resources for the worst case, we should (and will in the next article) also look at daily rates of change and, likely begin to shift from exponential to linear regression to see a better fit.

As it stands, which hospitals are prepared for the incoming influx of patients and which hospitals will struggle to meet increased demand? To answer this question, we analyzed data at the county level using the same methodology as in our last as our last article in which we used Imperial College London’s prediction for cases with all, none and some precautions taken to prevent spread. We will attach our findings in a spreadsheet however, here is a sample of our data and some takeaways. For our example, we will look at Alabama again.

Supply vs Demand of Beds Available in Alabama – Worst Case Scenario

Fig 1: The above figure shows Supply minus Demand at peak when no precautions are taken to prevent spread. All counties appearing above the red dashed line have capacity, even at peak. All Counties at or falling below the red line are will not be able to meet demand. In this scenario, peak will hit mid-May. Planning for servicing counties that either do not have hospitals or have overburdened systems should be made. Some counties will have capacity to redirect to needed areas.

Fig 2: In the more likely scenario where some precautions are taken to flatten the curve, data suggests some counties will still be unable to meet the needed demand. The peak will hit in early June. Planning for servicing counties that either do not have hospitals or have overburdened systems should be made. Some counties will have the capacity to redirect to needed areas.

Supply vs Demand of Beds Available in Alabama – Most Likely Scenario

Fig 3: In the scenario where all precautions are taken to flatten the curve, data suggests almost all counties will be able to meet the needed demand. The peak will hit in June. Planning for servicing counties that either do not have hospitals or have overburdened systems should be made. Several counties will have capacity to redirect to needed areas.

Supply vs Demand of Beds Available in Alabama – Best Case Scenario

These figures give us a way to visually see which counties will be overwhelmed by the demand for beds amidst the Covid-19 Pandemic. They show us that there are many counties that can handle the demand if all preventative measures are taken but a large majority will be overwhelmed if weight is not placed on prevention. Our attached spreadsheet flags these counties given their level of preventative measures in place.

Conclusion

Using exponential regression as a prediction tool is efficient in a worst-case scenario. This is likely a more useful tool in areas that are densely populated and experiencing a high infection rate. We can use these predictions as a first step in an attempt to estimate the demand for beds for those with the highest risk, Americans aged 65+ with preexisting conditions. Once we know that, we can then look at numbers at the state and county level to see which hospitals will be overwhelmed by demand and require redirected resources. These are likely the last few days we can rely on exponential regression before switching over to linear regression as a more accurate and reliable tool.

As we concluded in our last article, we strongly believe that efforts to minimize infection rates such as closing schools, non-essential businesses, practicing social distancing, handwashing, etc., are key to preventing the overwhelming of hospital resources. Furthermore, we are including an attachment showing our predictions at each county level by the state for which hospitals are likely to see more demand than the available supply. It is our hope that this information can be used to funnel resources from hospitals with excess demand to those that will be overwhelmed by new patients.

In our first article, we reference a study from Imperial College London that will give us a better idea of which curve (i.e., some precautions, no precautions, all precautions taken) we are following. We will continue to compare this to new data as it surfaces. Finally, to circle back to our last article – once we have a predicted number of total cases at a smaller level, we can begin to predict the needs of those at a higher risk of being admitted to the hospital with preexisting conditions. From CDC data, we can anticipate that 30% of Covid-19 cases will be patients aged 65+. Of that population, we can utilize the data from CMS mentioned in our last article to anticipate medical device and physician demand for patients with preexisting conditions such as diabetes, heart disease, and COPD.

Citations

Covid-19 cases by day, USA:

“United States.” Worldometer, www.worldometers.info/coronavirus/country/us/.

Covid-19 cases by day, New York and Alabama:

Project, The COVID19 Tracking. “Most Recent Data.” The COVID Tracking Project, covidtracking.com/data/.

Demand vs Supply Charts: Created by author(s) using data from the CDC and census.gov

Tracking Covid-19 Resource Requirements Across the US Healthcare System

by Jolly Nanda | Mar 28, 2020 | Covid

Tracking Covid-19 Resource Requirements Across the US Healthcare System
Ayesha Rajan, Research Analyst at Altheia Predictive Health

Background

In this article we are discussing findings and inferences from 1.3 million outpatient records provided by the Centers for Medicaid and Medicare Services (“CMS”). The data set includes the records of Medicare patients with a mix of chronic conditions seen for outpatient encounters in the past 3 years. We are applying our findings to identify the kinds of patients that are at a higher risk for contracting the Coronavirus disease 2019, also known as Covid-19. Given the fact that Italy has been hit especially hard by Covid-19 due to its vast elderly population, the analysis of our own elderly American population is important for both preparation and prevention. 

Findings

Since all the patients in our sample are participants in Medicare, we know that the vast majority are already part of the at-risk group. The Centers for Disease Control (“CDC”) has also identified those who have Heart Disease and Diabetes to be at an increased risk of contracting Covid-19, as well as anyone with a serious underlying medical condition such as Chronic Obstructive Pulmonary Disease (“COPD”).

The CDC has already published that 8 out of 10 deaths reported in the U.S. have been in adults 65 years of age and older. Using the 2019 census data, which provides that the U.S. population is 328.23 million, we can infer that 16% of the total population of the U.S. or 52.5 million people are vulnerable. Co-morbidity of this population with COPD and Diabetes Mellitus (“DM”) or Coronary Artery Disease (“CAD”) elevates this risk.

We have been working with Medicare data for researching and refining algorithms to create better predictive models for chronic diseases.  With the outbreak of Covid-19, we though it vital to share our findings of the co-morbid conditions and Covid-19 to create better preparedness.

What we were able to extract from our data set of 1,315,025 patient records is the percentages of people with overlapping preexisting conditions.  Listed below are those that occur most frequently, translated from percentages to real numbers. Amongst an elderly US population, the groups of patients with DM with COPD and those with CAD with COPD are at the highest risk if exposed to Covid-19 (see Figure 2).

Figure 2

Hospitalization, ICU admissions and Deaths

We then looked at the CDC chart below for Hospitalization, ICU admissions and Deaths, which support the identification of the elderly as being at a significantly high risk for mortality.

Vulnerable Population by State

We also analyzed publicly available data from the CDC and Census data by State to identify hot spots by total population over 60 years of age, and to identify COPD, DM, Heart Disease and Cancer. The chart below shows areas where we predict an overflow of healthcare needs.

Imperial College Model

The Imperial College Covid-19 Response Team published a model that shows that even with flattening the curve with voluntary quarantine, closure of schools, including colleges and universities, social distancing of entire populations, including and especially the elderly and vulnerable, we only succeed at lowering the curve.  We are just at the onset of the upward curve. The “light blue” line shows that we will peak in critical care bed needs by mid-June 2020.

Hospital Beds – Supply vs. Demand

Looking at the data, as many healthcare professionals are predicting, hospitals will soon be overwhelmed by Covid-19 patients, many of whom will have one or more preexisting conditions.

Hospitals are already trying to increase their supplies of respiratory machines, but that alone will not help if an influx of patients that arrive in need of other treatment, including insulin, dialysis or attention to coronary issues.  As hospitals prepare to increase the resources available to treat Covid-19 patients, they must also consider that many of these patients will need other types of medical treatment. This additional care will create expenses that insurance companies (including Medicare) will have to factor into its cost projections.

Hospital Beds – Supply vs. Demand with Precautions

If precautions are put in place to manage the spread of Covid-19, we will see that peak demand will occur in June, but that demand will be comfortably met by every state. However, if we do not take the necessary precautions of quarantine, social distancing and closing businesses with a broad brush, we can expect there to be peaks in demand for hospital beds that will not be met. Below we can see figures that represent the demand for hospital beds if some action is taken and if no action at all is taken. While the peaks are further apart if some action is taken, many states will still face overwhelming demand.

If some precautions are taken, we will see that peak demand will hit in June. At that time states like Colorado, Idaho, New Hampshire, Oregon, Utah, Vermont and Washington will no longer have enough beds to meet demand. States like Alaska, Hawaii, Maine, Montana, New Mexico, North Dakota, Rhode Island and Wyoming are at risk of finding themselves the same predicament.

Hospital Beds – Supply vs. Demand with No Precautions

If no precautions are taken, we will see peak demand in mid-May at which time the demand for hospital beds will be higher than the available number of beds in nearly every state.

Conclusion

In reviewing all published data, we strongly support the decisions to close schools, including colleges and universities, cancel all non-essential services and continue to practice social distancing across all ages. We can see that without these measures, hospitals in many states face high demand for beds with limited supply.

The CDC states that the high-risk group of Americans aged 65 years of age and older comprises 31% of Covid-19 cases.  Therefore, as the number of these patients increase, it is key to factor in that many of these patients will need treatment for other medical issues, such as COPD, CAD or DM, in addition to their treatment for Covid-19.

Further analysis can be conducted at the county level across the U.S. to identify shortages of critical healthcare assets. This is essential to ensuring medical treatment, supplies and transportation and evacuation services are in place to meet projected demand.

We will continue to analyze the data and publish this county level data within a few days.

Citations

Figure 1: Johns Hopkins via Vox.com

Animashaun, Christina, and Kelsey Piper. “Why We’re Not Overreacting to the Coronavirus, in One Chart.” Vox, Vox, 20 Mar. 2020, www.vox.com/future-perfect/2020/3/20/21179040/coronavirus-us-italy-not-overreacting.

Figure 2: Created by author using Census Data by State

 

Figure 3: Total Population versus Vulnerable (Per CDC 65+ and then looking at 65+ with Diabetes, Coronary Artery Disease and COPD, Co-morbidity of COPD with DM and CAD from CDC Data

Figure 4: CDC via Fox News;

Hein, Alexandria. “8 In 10 Coronavirus-Related Deaths in US Involve Older Adults: CDC.” Fox News, FOX News Network, 19 Mar. 2020, www.foxnews.com/health/8-in-10-coronavirus-related-deaths-us-involve-older-adults-cdc.

Figure 5, 7, 8, 9: Created by author(s) using data from the CDC and census.gov

Figure 6: Imperial College London

Ferguson, Neil. “Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID- 19 Mortality and Healthcare Demand.” Https://Www.imperial.ac.uk, 2020, www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-NPI-modelling-16-03-2020.pdf.

Additional Information

Figure 7 and 8 may appear to be missing data, however, the values were too small to be seen on the graph.

Below is the full table of data used.

For Figure 7 Table Below was used.

For Figure 8, the following table was used:

Covid 19 Projections

by Jolly Nanda | Mar 28, 2020 | Covid

Different parts of the country are seeing different levels of COVID-19 activity. The United States nationally is in the acceleration phase of the pandemic.  The duration and severity of each pandemic phase can vary depending on the characteristics of the virus and each state’s public health response.

These projections measure the demand and supply of hospital beds based on the level of precautions taken:

Read Altheia’s white papers on these predictive analytics at:
“Tracking Covid-19 Resource Requirements Across the US Healthcare System“
and
“Predicting the Effect of Covid-19 on the US Population and Healthcare System“

For an Interactive Visualization of this data: Download Here (Microsoft Power BI app must be installed)
Excel Data File: Download Here

Alabama

Alaska

Arizona

Arkansas

California

Colorado

Connecticut

Delaware

Florida

Georgia

Hawaii

Idaho

Illinois

Indiana

Iowa

Kansas

Kentucky

Louisiana

Maine

Maryland

Massachusetts

Michigan

Minnesota

Mississippi

Missouri

Montana

Nebraska

Nevada

New Hampshire

New Jersey

New Mexico

New York

North Carolina

North Dakota

Ohio

Oklahoma

Oregon

Pennsylvania

Rhode Island

South Carolina

South Dakota

Tennessee

Texas

Utah

Vermont

Virginia

Washington

West Virginia

Wisconsin

Wyoming